Lies, Damned Lies, Vaccine Statistics, and Eric Topol
When the real numbers get in your way, just invent your own and spread dangerous misinformation
Part Two of One
I didn’t intend to make a series out of my previous article. I was hoping it would be more self contained. Stand on its own. But circumstances change, and here I am writing part two.
If you take away the specific study and math discussed last time, there were several points comprising the main argument of part one:
Pro universal-vaccination statistics are widely accepted regardless of accuracy or correct interpretation
Overstating protection is viewed as acceptable, if it encourages vaccination
The bad statistics encourage behavior that increases risk of infection among the vaccinated by overstating protection
The bad statistics leave people unprepared to analyze real world results as they come out — leading to confusion and incorrect interpretations
The last article focused on severely misunderstood statistics. Today I am focusing on what can only be described as a deliberate lie.
Category 6 - Acceptable Catastrophic Error Storm
As I wrote last time, universal-vaccination advocates are permitted to use any numbers they choose, regardless of how well they match reality. Today’s example is an impressive tour de force of falsehood. This example contains
Cherry picked data
Getting the cherry-picked data wrong by an order of magnitude
Comparing the cherry-picked data against other data that do not represent what they are claimed to represent
All of which will be permitted, and repeated, because they promote universal-vaccination. They are Acceptable Catastrophic Errors.
Eric Topol
Today’s offender is fairly accomplished.
Topol has published over 1,200 peer-reviewed articles, with more than 310,000 citations, h-index 235, elected to the National Academy of Medicine, and is one of the top 10 most cited researchers in medicine. His principal scientific focus has been on the genomic and digital tools, with the use of artificial intelligence analytics, to individualize medicine. He also pioneered the development of many medications that are routinely used in medical practice including t-PA, Plavix, Angiomax, and ReoPro. He has led clinical trials in over 40 countries involving over 200,000 patients
Recently, Sam Harris invited Eric on his Waking Up podcast for an episode titled "A Contagion of Bad Ideas.” It was Harris’ stated intent on that podcast to build the strongest case possible for universal-vaccination, with Eric Topol chosen by Harris as the guest most up to the task.
Topol was sloppy enough on that podcast with data. But one may excuse that as being a verbal discussion. Today however we have something Eric deliberately constructed for his audiences to consume. Numbers he asserts are real with math he asserts is correct.
The Offending Tweets


Parsing the Tweets1, which are a little haphazard, we have Eric proposing that “if 10% of fully vaccinated people got [a Delta breakthrough], and we apply 1.2% getting hospitalized […] Then 99.88% of vaccinated people would be protected from hospitalizations.”
In this setup we have an unknown number of fully vaccinated people, and we take 10% of them and say they got a Delta breakthrough. This gives us some unknown number of infected. Now we have 1.2% of the infected go on to be hospitalized. Eric then asserts this is 99.88% protection from hospitalization.
Well, for sure, 10% times 1.2% when subtracted from 100% is 99.88%. Eric claims this entire 99.88% was protected by the vaccine from hospitalization. This claim is a bit spurious, as, while we’re inventing scenarios, if 10% of the unvaccinated came down with a Delta infection, and 1.2% of them were hospitalized, we wouldn’t say they were protected by anything. Crediting all positive outcomes, but never the negative ones, to the vaccine is arbitrary and lacks meaning.
Eric then follows up with a direct comparison to unvaccinated groups, which would be more meaningful than his first attempt. He uses the proportion 1.2/1000, which can be obtained by his previous setup. 10% of 1000 vaccinated people is 100 infected, and 1.2% of that is, well, 1.2 hospitalized.
And lo and behold, 16/1000, which he says comes from his included table, is over 10 times the rate of 1.2/1000. The vaccine has provided over 10 times the protection from hospitalization if infected with the Delta variant, versus being unvaccinated.
Acceptable Catastrophic Error: Category 1
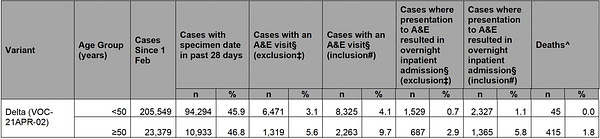
The first problem with his calculation is a bit of sleight of hand. To arrive at his number of comparison for the unvaccinated, 16/1000, we will turn to his provided table.
If we divide the sum of the numbers under the blue arrow (Delta hospitalizations) by the numbers under the red arrow (Delta cases) we get:
This is where his 16/1000 number comes from. We divided the number of hospitalizations by the number of cases.
The number Eric uses for the vaccinated group, 1.2/1000, is not the number of hospitalizations by the number of cases. It is the number of hospitalizations divided by the number of vaccinated people. This is a sleight of hand trick that allows him to misinform about the conditional layers of protection by an order of magnitude.
Correcting for this, still using his numbers under his setup, we would get 12/1000. This means no longer have the infected unvaccinated group been hospitalized at over 10 times the rate of the infected vaccinated group.
We now only have the infected unvaccinated group hospitalized 1.33 times the rate of infected vaccinated group. An order of magnitude difference.
Of course, this is an Acceptable Catastrophic Error.
Acceptable Catastrophic Error: Category 2
This 1.2% number comes from “Provincetown Data.”
During July 2021, 469 cases of COVID-19 associated with multiple summer events and large public gatherings in a town in Barnstable County, Massachusetts, were identified among Massachusetts residents; vaccination coverage among eligible Massachusetts residents was 69%. Approximately three quarters (346; 74%) of cases occurred in fully vaccinated persons (those who had completed a 2-dose course of mRNA vaccine [Pfizer-BioNTech or Moderna] or had received a single dose of Janssen [Johnson & Johnson] vaccine ≥14 days before exposure). Genomic sequencing of specimens from 133 patients identified the B.1.617.2 (Delta) variant of SARS-CoV-2, the virus that causes COVID-19, in 119 (89%) and the Delta AY.3 sublineage in one (1%). Overall, 274 (79%) vaccinated patients with breakthrough infection were symptomatic. Among five COVID-19 patients who were hospitalized, four were fully vaccinated; no deaths were reported.
Four fully vaccinated hospitalizations out of 346 fully vaccinated infections. This gives you indeed a 1.2% infection hospitalization rate2.
But using this same data source to calculate the infection hospitalization rate for the unvaccinated gives you a 0.8% infection hospitalization rate.
The infection hospitalization rate among the vaccinated is approximately 1.42 times higher than that of the unvaccinated in his primary data set.
But, of course, this is an Acceptable Catastrophic Error.
Acceptable Catastrophic Error: Category 3
The figure 12/1000 comes from an extremely small set of observations. This was one small town over one small time period. It wouldn’t be generally advisable to extrapolate these tiny results and consider this 1.2% number fixed.
With observations this small, there is an extraordinary amount of uncertainty in estimation. It is not appropriate to leave out this much uncertainty to make predictions and comparisons. And when you try to incorporate that uncertainty, the results show that the rate could easily be higher than 16/1000.
What you are looking at is a graph of various infection hospitalization rates that are compatible with the observation 4 in 346. The higher the line on the graph, the more compatible that rate is with the observations.
This allows us to measure the “area under the curve” to compare two different ranges of estimates, and see which are more likely (based on how little we know).
The blue shaded area is the area that is greater than 16/1000. It is approximately 26% of the total area of this estimate3. That means, based on the little information we have, there is 26% chance the infection hospitalization rate of the vaccinated group is higher than 16/1000.
Yes, there is a 74% chance, based on what little we know, that the rate is lower than 16/1000, but when trying to demonstrate how certain you are about the vaccine’s performance in different scenarios, you might not want to use data that winds up sounding like a scene from The Naked Gun.
Eric told us it was 1.2/1000 when instead it was 12/1000. And that 12/1000 was based on so little data, there is a 26% chance of the real rate4 being higher than the 16/1000 number Eric compared it to.
But, of course, this is an Acceptable Catastrophic Error.
Acceptable Catastrophic Error: Category 4
The data Eric uses from the UK is not what he claims. The data is a mixture of unvaccinated and vaccinated Delta cases. I spotted this immediately because I had been through the very same data set he was referencing when I wrote part one.
The data comes from a document “SARS-CoV-2 variants of concern and variants under investigation in England.” Specifically, his data comes from Table 4 on page 14 titled “Attendance to emergency care and deaths among all sequenced and genotyped COVID-19 cases in England, 1 February 2021 to 19 July 2021.”
Sure enough, this table does break down COVID variants. But it does not distinguish between vaccinated and unvaccinated people.
But table 5 on page 18 does. Eric must have known the very next table on page 18, titled “Attendance to emergency care and deaths by vaccination status among all sequenced and genotyped Delta cases in England from 1 February 2021 to 19 July 2021” [emphasis mine] contained all the information necessary to make the Delta vaccinated/unvaccinated infection hospitalization rate comparison.
That table is a bit long, so I have taken the liberty to condense the rows to only what we need.
The Total Cases, under the red arrow match Eric’s original <50 and ≥50 numbers. They do not exactly sum to All Cases directly below, because they have some cases with no age data available, according to a footnote5. But if you see under the green arrow, the unvaccinated <50 Delta cases are almost half his original numbers and the unvaccinated ≥50 Delta cases are a tenth of his original numbers.
Using the correct values, and using the same column (now a row) as he used before, we can compare the infection hospitalization rate for both vaccinated and unvaccinated Delta cases. The infection hospitalization rate for the vaccinated (received two doses):
And the unvaccinated:
The vaccinated infection hospitalization rate is 1.66 times that of the unvaccinated for Delta cases across all ages. It should be noted that 2.9% is over twice what Eric described in his original tweet as a worst case scenario.
But, of course, this is an Acceptable Catastrophic Error.
Acceptable Catastrophic Error: Category 5
Eric would probably object to the first critique of his post. He would probably argue that his calculation of 1.2/1000 (instead of 12/1000) is the correct comparison, because the vaccines are stopping 90% of people from getting infected. Therefore you should take the 1000 comparison number, and treat them all “as if” they were infected, because if they were not vaccinated they would have been infected.
But that’s not true. Eric himself does not profess to believe the vaccines are 90% effective at preventing infection in all cases across time. He currently is on record as saying the number may be 60%.


If we allow for his sleight of hand trick to be used, but reformulate it using numbers he professes to actually believe to be accurate, we now have 1000 vaccinated people, 40% of whom become infected with Delta and 1.2% of those become hospitalized.
This rate (4.8/1000) is now 4 times that of his purported vaccinated infection hospitalization rate (1.2/1000) in his original example. Even if it is still intentionally deceptive.
But, of course, this is an Acceptable Catastrophic Error.
Acceptable Catastrophic Error: Category 6
The Provincetown data itself is a situation where there was negative observed efficacy of the vaccine against infection. Per the excerpt in Category 2, 69% of the population is vaccinated. Eric’s entire argument now uses 90% efficacy when he believes the real efficacy is 60%, and while the observed efficacy in the actual situation is negative.
According to Wikipedia, Provincetown has a summer population of 60,000. 69% vaccination rate among the population gives you 41400 vaccinated and 18600 unvaccinated.
There were 346 cases out of 41400 vaccinated people and 123 cases out of 18600 unvaccinated people. This gives you a negative 26.38% efficacy against infection. This means by using one result, 1.2% infection hospitalization rate, with completely arbitrary efficacy rates instead of the real observed ones, he is simply just making up numbers at will.
But, of course, this is an Acceptable Catastrophic Error.
The Top of Mount Wrong
There was not a single number in Eric’s tweets that was correct. Every single attempt to reconcile the numbers demonstrates yet another way his analysis was wrong.
He was off by an order of magnitude with his “Provincetown” data, by dividing hypothetical vaccinated people instead of infections. This was deliberate.
He called the 1.2% results from Provincetown the “worst case scenario” when other sources he used clearly showed over double this number.
The numbers he claimed were unvaccinated infection hospitalizations were a mixture of vaccinated and unvaccinated.
That source showed the infection hospitalization rate was higher in the vaccinated group.
Even allowing his deliberate misleading by dividing by people instead of infections, based on his own professed belief that the infection efficacy is 60% and not 90%, his original estimate was deliberately off by a factor of four.
The observed efficacy was negative in the same data that gave Eric the 1.2% number. Neither 90% nor 60% efficacy was available in the data he cherry picked the 1.2% number from. It was negative 26%.
Universal-vaccination advocates are permitted to do this. There are no standards.
I do not believe the negative 26% efficacy rate from infection is applicable as a rule. It is not my conclusion that the Delta variant is “more infectious” in the vaccinated. At least not that I have yet seen. But I do believe that the protection granted by the vaccines against infection is strongly related to other factors including behavior. It is at least possible to lose most or all of the protection benefit by increasing coronavirus exposure.
By universal-vaccination advocates continuing to spread misinformation, including but not limited to just making numbers off the top of their head, people who are vaccinated will be misled about exactly how the vaccine is protecting them. This will cause people to take increased risks of infection. This will then create a feedback loop where advocates make up worse numbers to counteract the real world results that they fear reduce the allure of getting vaccinated, which in turn will worsen the real world results by people being incorrect in their understanding.
Whether all of them are Delta is a bit uncertain. The papers says Delta was identified in 133 patients, but out vaccinated group is 346 people.
Beta posterior distribution with Jeffreys prior. Choice of uninformed prior will influence skew, but Jeffreys prior allows the posterior median to be closer to the maximum likelihood estimate assuming binomial distribution than Haldane’s Prior, for example.
There is no fixed “real rate.” Estimated rates are based on real people, who had real prior health statuses and genetics, that affect the viruses ability to affect the person. We try to gather data to estimate “rates.” These estimates may be useful to make some predictions, as sometimes large groups of people will have similar characteristics in similar proportions - but the underlying conditions are always changing, and one should never assume there is a true “rate” that future observations are beholden to forever.
The footnote reads: Age <50 ≥50 do not total ‘all cases’ per category as some cases lack reported age data




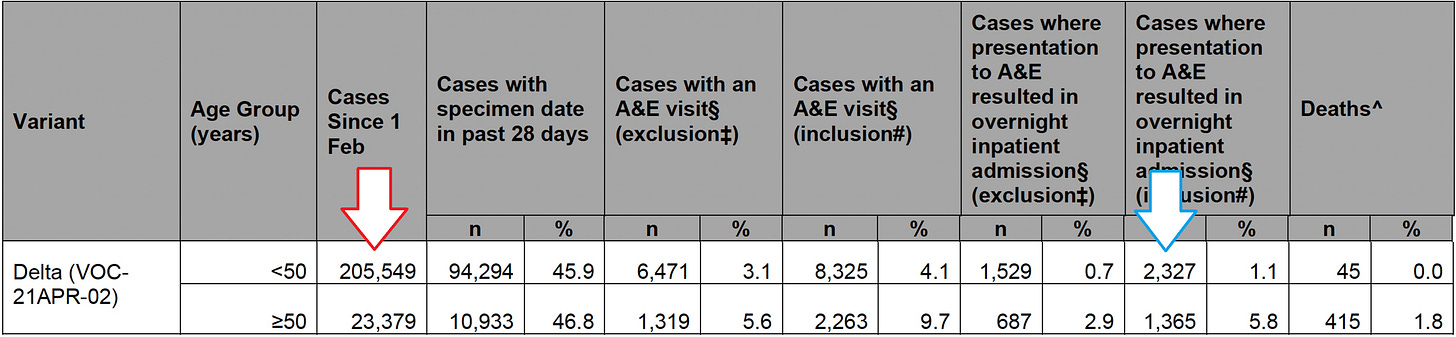













Looking at the UK data pg 18-19, >= 50 group, Received 2 doses vs. Unvaccinated appears to show a very strong protection against death. I calculate the case fatality rate as 1.638% for vaccinated against 5.605% unvaccinated. The under 50 age group is basically a wash on case fatality rate; perhaps a very slight benefit to vaccination. Do you agree with that observation?